First and foremost, I want to thank @Avantgarde for putting forth this treasury growth proposal for the Compound DAO and for thoughtfully incorporating multiple rounds of community feedback.
Combining a covered call strategy with lending yield and buybacks to create a positive flywheel for the treasury is a creative idea that should be commended.
Platonia committed to delivering quantitative analysis on this opportunity in a recent community call, with a primary focus on the covered call portion of the proposal. I further want to emphasize that any subsequent feedback here is not intended to impede progress at the 11th hour but rather call to attention execution details that will become increasingly important when scaling up the strategy in the future.
The remainder of this post will be structured as follows
- Requests for clarification
- Options execution challenges
- A utility framework for decision making
Requests for clarification
Some of the following technical details may have been left out from the proposal for clarity and accessibility for the broader community. Surfacing them here will be valuable for developing a technical understanding of how the strategy can succeed at scale.
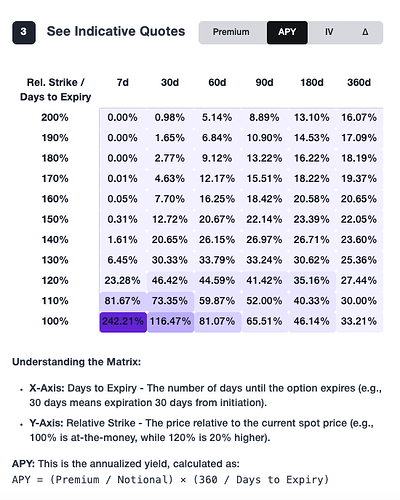
- What was the COMP price used for the indicative quotes given? Alternatively what were the implied volatilities (IVs) quoted? The fairness of the quotes is difficult to assess without one or the other. The remainder of the post uses a COMP price of $40 (roughly the price when the indicative quote was first posted in the forum here) as a reference point which corresponds to an IV of ~160% for the 90d and ~135% for the 180d options.
- How will settlement prices for COMP be determined on MYSO? Are there specific oracles or methodologies the community can review? From MYSO V3’s contracts, it seems like there is an oracle dependency here in the Escrow contract which eventually queries a Chainlink oracle here.
- Are there any more details Avantgarde can provide on the execution timing and sizing of the covered call strategy?
- It’s been stated that there’s confirmed interest from institutional trading firms. Is there a formal agreement in place with market maker(s) on MYSO? If so, what are the parameters of the agreement? Asking since recent indicative quotes for these calls on the MYSO front end show an IV of less than 80% corresponding to a premium of only 0.1% APY.
Generally MYSO’s indicative pricing seems to show low premiums and APYs for deep out of the money calls.
MYSO’s indicative IVs also seem relatively low given the annualized realized volatility of COMP has been around 110% (computed from standard deviation of daily log returns from the past 180 days)
but still far below the IVs of ~160% possibly implied by the indicative quotes from the market maker. - Mind sharing who the market maker(s) are? With only indicative quotes to go on, a customized options trade like this requires a higher degree of trust, so knowing the reputability of the counterparty would be reassuring.
- How will execution quality be measured?
- Are there indicative quotes available for the cUSDC put writing strategy? Will these transactions also take place on MYSO? Asking because the MYSO smart contracts seem to support writing cash-secured puts and they are mentioned here, but unlike for writing covered calls, no indicative quotes seem to be available on the front end.
- Is there historical trade data available on MYSO, especially any transactions on COMP covered calls and cUSDC cash secured puts on COMP or involving the expected counterparties for these trades?
Initial attempts to answer some of these are included below but it would be helpful to get @Avantgarde’s insights as well.
Execution challenges
The benefits of writing covered calls on COMP seem well understood in terms of generating additional yield in exchange for some of the tail upside. There are a lot of potential costs to executing such a strategy which would be good to review.
Review
Option pricing
A theoretical price for European options is given by Black-Scholes which gives the value of a call as where
and
, C is the value of the call, N is the cumulative distribution function of the Normal distribution, S is the spot price, K is the strike price, r is the risk free rate, t is the time to expiry and σ is the annualized volatility of the asset.
When assessing an options quote the implied volatility can be derived from the market price using Black-Scholes. A common phenomenon is that deep out of the money (OTM) options tend to be priced with higher IVs than their at the money (ATM) counterparts. This pattern is often referred to as the volatility smile.
Capital efficiency
While options are viewed as highly capital efficient derivatives in TradFi as they allow for high leverage positions with low margin requirements, they are very capital inefficient in DeFi. In TradFi, this efficiency is underpinned by trust in centralized financial infrastructure, such as the Options Clearing Corporation (OCC), which holds a top-tier credit rating and guarantees the settlement of U.S.-listed options by acting as the counterparty to every trade.
In DeFi, by contrast, trust is not assumed between anonymous participants. As a result, both buyers and sellers typically must lock substantial collateral into escrow contracts, with full collateralization in the case of MYSO V3. Under current designs, the option seller forgoes any yield that could otherwise be earned on the locked assets (e.g. COMP staking). This is likely why on-chain DeFi options have, to date, been sold primarily by retail participants, with market makers mostly on the buy side.
Liquidity
Liquidity is a key consideration of any execution strategy, especially trading illiquid assets. Unfortunately, there does not appear to be a liquid market for COMP options on any open electronic exchange, which likely explains why MYSO was brought in to facilitate direct matching with institutional trading firms.
The most liquid crypto options exchange is Deribit which accounts for ~85% of global open interest. However, the vast majority of this volume is concentrated in BTC and ETH options, with limited markets for other assets like SOL, XRP, BNB, and PAXG. Even for ETH, deep OTM calls on Deribit tend to have very limited liquidity where spreads often exceed 15% and only a few hundred dollars are available at the best bid and offer.
Options market making
Market makers provide continuous buy and sell quotes to ensure liquidity in financial markets, profiting from the bid-ask spread while managing inventory risk. Because providing liquidity is more complex problem than pure arbitrage, options market makers bear all the costs of arbitrageurs as described here in addition to dealing with pricing uncertainty, delta hedging costs, idiosyncratic tail risk and development overhead, some of which will be described in more detail.
Options are highly leveraged instruments, making risk management through hedging essential. The most basic approach is delta hedging, where the spot asset is traded to neutralize the delta of the option position. This can be particularly costly if the underlying asset is illiquid. In COMP’s case, where average daily turnover is only ~900,000 tokens, market makers are heavily constrained in the size of the options positions they can write without incurring substantial inventory risk.
In addition to inventory and hedging constraints, the MYSO auction mechanism itself can introduce additional overhead. While Dutch auctions offer a simple and transparent method for price discovery, they impose a tax on market makers in the form of development time (for modeling and integration) as well as operational attentiveness. For a trader to engage, the auction should roughly be one of the most attractive opportunities in the market over its duration which is not always guaranteed.
Ultimately, all of these costs are priced into a market maker’s quote to ensure profitability, which is reflected in the overall execution cost of the options strategy.
Execution baseline
The proposal mentions targeting a 15% annualized option premium but would benefit from more detail on how execution quality will be evaluated. While the premium received from writing calls is always positive in nominal terms, what ultimately matters is whether that premium is fair relative to the expected value of the options being sold.
As it stands, there is no constraint preventing the sale of deep OTM calls at low prices to meet the premium target while bearing a negative expected return. This is analogous to the impermanent loss Uniswap LPs face impermanent loss who are effectively short volatility. Similarly, writing covered calls realizes losses when the calls are exercised in the money following a price increase.
To evaluate performance meaningfully, premiums should be benchmarked against a fair market value for the options. Realistically, if there is limited retail demand for COMP speculation and the counterparty is consistently a sophisticated trading firm, the strategy is likely to have negative expected value (–EV). That can still be acceptable if the downside is well-understood and reasonably bounded.
Risks
High execution costs
The primary risk to this strategy is simply that the execution costs may prove up too high relative to the premium, driven largely by costs borne from by the market maker, and to a smaller extent, the treasury.
Several factors contribute to elevated costs for the market maker:
- Substantial inventory risk and pricing uncertainty given the absence of a COMP options market on exchange
- High delta hedging costs from greater market impact in an illiquid COMP spot market
- Operational and labor demands in the form of trader attention and dev integration cycles for the Dutch auction and research bandwidth into a pricing model
These costs are likely to be passed on to the treasury through wider spreads or less favorable execution. Since this is a highly bespoke market that doesn’t exist elsewhere, market makers hold significant pricing power and may effectively name their price.
Encouragingly, the indicative quotes received so far appear more favorable than expected, showing a ~200x improvement over MYSO’s quotes in some cases, as seen in the screenshots above. If that pricing holds at execution, it would be a great outcome. However, indicative quotes are by definition non-binding and subject to change, especially at larger trade sizes. Any meaningful deviation from those initial quotes could materially impact the overall execution cost of this strategy.
One way to mitigate this risk is to ensure healthy competition among market makers. Gathering indicative quotes from multiple reputable firms would help demonstrate that the auction will draw real participation. Alternatively, a bilateral agreement could be made with a designated market maker, specifying that the final execution price must fall within a defined range of a pre-agreed pricing model baseline.
It’s important for the treasury to retain any future staking yield from COMP. The simplest approach would be to incorporate this yield into the option premium, though this would require agreement from the buyer. Smart contract solutions exist that could address this (e.g. deliver a Pendle principal token at expiration while the treasury retains the yield token) but these will take time to validate in practice. Moreover, DeFi options volume are still a small fraction of spot and perpetual trading volumes, and there is no real precedent for trading options on staked assets.
Given these constraints, the DAO should anticipate an interim period during which covered call yield excludes staking yield. Both the technical infrastructure and a willing set of counterparties for staked COMP options will need to emerge before such integrations are viable.
The proposal also has 15% of option premiums as compensation which is another contributor to overall execution costs.
Settlement price manipulation
One form of market manipulation involves aggressively trading an asset to influence its settlement price just before expiration. This is sometimes referred to as banging the close. As a hypothetical example, suppose that calls were written on 40k COMP tokens at a strike of $130 and COMP is trading at exactly $130 just before expiration. If the call buyer pushed the price of COMP from $130 to $140 right at the last moment, the calls would finish in the money, allowing the buyer to pocket $400k on options that would have otherwise expired worthless.
To mitigate this kind of manipulation, settlement prices in TradFi are often based on a weighted average price or involve a highly liquid auction like the Nasdaq closing cross. Any oracle used for options settlement should probably adopt similar safeguards to ensure robustness to this type of economic exploit. This risk can also be reduced by staggering options expirations over time, ensuring that no single expiry is large enough to create a profitable manipulation opportunity.
Frontrunning
Another form of price manipulation is frontrunning. If the parameters of a strategy are static, public and therefore predictable, an actor could exploit this to their advantage.
Suppose a call buyer knows that the treasury is targeting a 20% premium on 40k COMP tokens and COMP is trading at $40. At an IV of 165%, this corresponds to writing about 40k OTM calls at a $130 strike with 90 days to expiration (DTE). While there is no COMP options market to frontrun directly, if a buyer knows when an auction will begin, they can move the underlying spot price in their favor.
For example, the buyer could push COMP down to $35 just before the auction. Now, to earn 20% at the same IV, the treasury would need to write 40k OTM calls at roughly a $107 strike with 90 DTE. After the auction, the buyer pushes COMP back to $40 and pockets ~$40k in option value they wouldn’t have otherwise captured. This translates to a 10% annualized loss on capital for the treasury. The larger the trade size, the more profitable this becomes, since the cost to move COMP down is relatively fixed if there’s no change in spot liquidity, while the profit from frontrunning scales with notional size.
This risk can be reduced by executing in smaller chunks and using an average price oracle to determine the spot reference for pricing.
Main takeaway
This strategy has potential, but there are several important risks that need to be managed carefully. In summary:
- Execution costs could be significant. This is a bespoke trade with no active COMP options market on exchange and an illiquid spot market. A lot is riding on the indicative quotes provided, which are around 200x better than MYSO’s. However, these quotes are non-binding, and market makers have considerable pricing power in this context. To reduce the risk of execution costs ballooning, especially at scale, it would be prudent to gather additional indicative quotes or expressions of interest from other reputable market makers and encourage healthy competition. Another approach is to form a bilateral agreement with a designated market maker, using a predetermined pricing model to set clear bounds for acceptable execution.
- Robustness against manipulation is critical. Common economic exploits such as frontrunning and settlement price manipulation could lead to substantial losses for the treasury. These risks can be addressed by executing gradually in smaller chunks over time and using weighted average oracles to determine the spot price input used for auctions and option settlement.
- Metrics for execution quality are essential. Without clear benchmarks, the treasury risks bleeding excessively from execution costs. Tracking effective yield relative to model-based fair value can help ensure the strategy is delivering net positive returns over time.
Utility framework
Just because a strategy is negative expected value (–EV) doesn’t necessarily mean it’s not worth pursuing. Insurance is a classic example: it loses in expectation, but it provides valuable protection against tail risk. Covered calls follow a similar logic, delivering additional yield while only giving up upside in favorable cases where the asset appreciates substantially.
One way to assess whether this tradeoff is worthwhile is by evaluating the strategy through a utility lens rather than purely in terms of expected wealth. This shifts the focus from maximizing average returns to optimizing outcomes in a way that aligns with the DAO’s overall risk preferences and strategic goals.
Overview
Risk aversion
Risk aversion is the willingness to give up some EV in exchange for reduced uncertainty. Most individuals and organizations are risk averse, and the degree of aversion increases with the size of the potential loss. For example, the DAO might easily accept a fair coin flip where heads yields a $50 gain and tails a $50 loss but would almost certainly decline the same flip if it involved $50 million.
This behavior is closely tied to the concept of diminishing marginal utility of wealth where the more wealth one has, the less utility is gained from each additional dollar. As a result, losses tend to feel more painful than equivalent gains feel rewarding.
Utility functions
Risk aversion can be expressed through a utility function, which translates wealth into utility. One canonical example is the isoelastic utility function defined as
This has the property of constant relative risk aversion (CRRA) where
which is to say that risk aversion is determined by the size of the risk relative to wealth.
Another common utility function is the exponential utility function defined as
which exhibits constant absolute risk aversion (CARA) where
so risk aversion is determined by the absolute size of the risk, independent of wealth.
Some possible utility functions for the treasury are plotted below:
Note that the utility values on the y-axis can vary significantly depending on parameterization. The important takeaway is that utility functions allow for relative comparisons e.g. U(A)>U(B) implies that A is preferred over B. However, absolute comparisons like U(A)−U(B) are generally not meaningful on their own.
Applications
Treasury decision making
Utility functions can be a useful tool for guiding treasury management decisions. Instead of having to determine whether an initiative is positive expected value (+EV), it’s more straightforward to assess whether it results in a gain in expected utility (+EU).
Estimating EV typically requires deep quantitative insights about the market, whereas identifying whether a strategy is +EU often comes down to measuring risk and tracking transaction costs. As an example, volatility targeting is probably +EU since it reduces variance with relatively low rebalancing costs.
Some of the rationale for writing covered calls is based on diminishing marginal utility. Losses from these positions generally occur only after wealth has already increased, making them more acceptable. This can be viewed as rearranging wealth changes along the payoff curve to gain utility. In that light, selling upside calls around the point where marginal utility begins to flatten can be a +EU strategy for the treasury.
Strategy stackranking
Utility functions are also helpful for comparing the relative performance of different strategies. For a risk averse DAO, one potentially valuable approach is buying deep OTM puts, sometimes referred to as crash puts. While these cost a premium, they can function like insurance, improving outcomes during sharp downturns. Rearranging wealth from good outcomes to soften the impact of bad ones can be +EU.
Consider the following strategies applied to idle COMP in the treasury:
- Do nothing (idle COMP)
- Writing deep OTM calls on all the idle COMP, targeting a 20% annualized premium
- Writing OTM calls on half of the idle COMP, targeting a 20% annualized premium
- Buy deep OTM puts on all the idle COMP, targeting a 10% annualized premium cost
- Do 2 and 4
- Do 3 and 4
- Write cash secured OTM puts sized for 25% of idle COMP, targeting a 15% annualized premium
To put some numbers to this, assume COMP is trading at $40 and all options have 90 DTE. Below is a table of strike prices that roughly fit the desired option sizing, premium target and strike ranges as IVs change.
| IVs ↓ \ Strategies → | Deep OTM Call | OTM Call | OTM Put | Deep OTM Put |
|---|---|---|---|---|
| 80% | $57 | $47 | $39 | $26 |
| 120% | $80 | $62 | $34 | $20 |
| 160% | $121 | $86 | $29 | $15 |
The chart below shows how utility changes with COMP price moves for each of the strategies, using an isoelastic utility function with γ=1. This corresponds to a logarithmic utility curve, which reflects moderate risk aversion. For this example, IV is fixed at 120% for the instant spot moves.
Some observations:
- Writing puts has the highest utility in the upmoves by a hair, edging out HODLing from collecting the premium. It has by far lowest utility in the downmoves due to the increased long delta over HODLing.
- Crash puts show a more pronounced increase in utility the bigger the price drop, offering strong protection in tail scenarios while only slightly reducing utility across the rest of the curve
- Writing calls further out of the money results in greater utility loss on the extreme upside. This is due to two effects: more contracts are written since the premium per contract is smaller, and these calls appreciate more rapidly as they approach the money. However, the conversion probability to realize losses is much lower
While the above plot provides intuition about how utility changes with instantaneous price moves, those changes in option value may be difficult to realize before expiration due to limited liquidity. A more practical insight comes from analyzing EU at expiration, when option payoffs are fully settled.
To explore this, the COMP price (S) at expiration is simulated using geometric Brownian motion so where
, S0 is the initial price, σ is the annualized volatility and t is the time to expiry.
Each plot below shows how the EU of each strategy varies with σ. Taken together, the set of plots illustrates how this relationship evolves across different levels of IV and risk aversion.
In reading these, note that risk aversion increases from left to right and IV increases from bottom to top.
Some observations
- When realized volatility exceeds implied volatility, crash puts outperform, especially for lower levels of risk aversion where the large gain on the puts overcomes the disutility of the high variance
- When realized volatility is lower than implied volatility, writing covered calls is the best strategy. The gap relative to other strategies widens as IV rises and shrinks with increasing risk aversion
- Lower risk aversion magnifies the difference between OTM calls and deep OTM calls at the extremities of volatility. Deep OTM calls are more favorable when volatility is moderate where they rarely get exercised but still generate meaningful premium.
- As IV decreases, crash puts become more effective in comparison since insurance is cheaper. As risk aversion decreases, EU remains relatively stable or even increases as annualized volatility rises while the performance of other strategies sharply decline.
- Put writing performs worse as both risk aversion and IV increase, where it is largely dominated by writing calls. This is because puts can substantially reduce utility by amplifying losses in the event of large COMP drawdowns. That said, buybacks can offer utility benefits that are more indirectly tied to wealth, such as signaling a value floor and reinforcing confidence within the community, though directly buying COMP on the open market may be more targeted in generating favorable market impact.
Main takeaway
Utility functions provide a framework for the DAO to make more informed decisions and quantitatively assess how different treasury management strategies perform in the context of the DAO’s risk preferences and strategic goals.
The space of potential +EU options strategies is large, with parameterization across strike selection, sizing, duration, option type and combinations thereof. While finding a seller may be difficult, crash puts can offer valuable protection in severe drawdowns. Exploring the possibility of purchasing them outright, or funding them using a portion of the yield from covered calls, may be worthwhile. Also, direct buybacks of spot COMP may be a more effective approach than writing puts, potentially leading to a more significant positive impact on COMP price.
The optimal options strategy can vary significantly with IV and risk aversion. This highlights the importance of the prices the options are executed at and the value of reaching community consensus on the proper degree of risk tolerance.
Hope this was a helpful overview.
Big thanks to @Avantgarde for the work behind this proposal and for bringing MYSO into the fold. Even with some open questions, this seems like a worthwhile experiment for the treasury to start gathering valuable real world data, akin to the Compound Morpho Polygon collaboration.
As with any initiative in DeFi, and especially one involving bespoke option strategies, it is important to remember that good results at small sizes do not necessarily translate at a larger scale. That consideration was one of the main motivations behind this analysis.
There were a number of suggestions included above, which could involve a fair amount of work, so happy to be of assistance—whether that involves joining meetings with market makers to assess indicative quotes or developing a pricing model. Feel free to reach out and also happy to discuss further on the next community call.