Hi, I’m Victor, and after sitting in on the recent developer community calls, I wanted to offer some (hopefully) clarifying thoughts and potential paths forward.
The need to raise collateral factors (CFs) in order to better compete in the DeFi lending marketplace is an important topic of discussion. It involves many intricacies and varied stakeholders viewpoints and as such warrants a structured response.
Based on the threads of conversation here and in this call, especially on the points raised by Alphagrowth and Gauntlet, I’m going to cover the following topics in order
- Risks to Compound III from increasing CFs
- Tradeoffs of various LRT oracles to the protocol and its users
- Design differences between Compound III and Aave V3 that affect leverage matching
- Possible next steps for driving more growth with the existing state and new features
Risks from raising CFs
The upside from having more aggressive CFs seems well understood in terms of increasing capital efficiency, which brings in elastic demand. The downside risks are well documented, but it doesn’t hurt to review them from first principles. Imagine a lot of this will be familiar to community members but the discussion gets deeper quickly so let’s start from the basics.
Review
Why overcollateralization
Compound is an overcollateralized lending protocol, so a requirement for opening a loan is that the value of the collateral posted exceeds the value of the borrow taken out of the protocol. If this were not the case, an adversarial actor could profit by borrowing all the assets with no intention of paying back the loans. With no real recourse against anonymous attackers or trust measures like a widely used onchain analogue of a credit score, the default assumption is that any shortfall between debt and collateral will be a loss fully borne by the protocol. This is commonly referred to as insolvency risk.
Liquidators
In order to protect against insolvency risk, the protocol incentivizes external actors, known as liquidators, to reduce the size of the balance sheet by purchasing collateral via debt repayment at a discount to the exchange rate. When collateralization has dropped sufficiently to render a loan liquidatable, anyone can call the smart contract to execute the liquidation.
Why liquidators fail
If liquidators always stepped in then there would never be any insolvencies. While there can be technical difficulties such as mempool congestion or extreme oracle updates, the primary reason for liquidators to not act is simply that it is unprofitable for them.
Liquidators have several costs including
- execution costs
- often slippage from atomically arbitraging using a DEX
- urgency to exit a position that was taken over because it has substantially dropped in value
- network costs
- gas
- MEV required to land the transaction
- labor costs
- is the expected payout worth the dev cycles
- opportunity cost
- e.g. if Aave is paying more prioritize liquidating there first
- if capital is tied up for awhile is their higher ROI elsewhere
If their share of the liquidation proceeds is insufficient to cover these costs, a liquidator is content to do nothing as the debt becomes insolvent.
Compound III bounds
In a Compound III liquidation, the collateral and debt of a loan are absorbed onto the protocol balance sheet, with the debt covered from the reserves. The amount of the borrow asset owed out to the user is their collateral value sans the liquidation penalty (LP). As such, we can derive the following relationship
![]()
where LF refers to the liquidation factor, the left hand side of the inequality is set to prevent opening loans that are immediately liquidatable and the right hand side is set to prevent absorptions that immediately lead to insolvent debt.
Let us define the insolvency buffer (IB) as the maximum % the collateral price can drop relative to the debt between absorption and sale before Compound III takes a loss. This was previously derived by Gauntlet as
![]()
where SFPF is the store front price factor.
When SFPF = 0, IB = LP and when SFPF = 1, IB = 0 and for all other cases the equation can be rewritten as
![]()
which is an increasing function in LP over [0, 1].
Thus, raising CFs lowers the maximum LP for an asset, which in turn reduces both the insolvency buffer and the payment for a liquidator to take over loans before they become underwater. Generally speaking [1], this leads to an increase in insolvency risk.
Risks
Insolvency
As repeated ad nauseum, the primary risk to a lending protocol are insolvencies where losses occur on overcollateralized loans when the borrow exceeds the value of the collateral. While infrequent, these can happen due to market events (such as depegs) or economic exploits (like an oracle price manipulation) and, in some cases act, as a death knell for a protocol, as seen in the example of Mango Markets below.
Bank run
Even when the monetary loss of insolvencies themselves are not that significant, they can lead to a crisis of faith in the protocol. In a space filled with memecoin casinos, lending is supposed to be a comparatively safe source of yield so any loss on principal could trigger withdrawals, which could escalate into a bank run.
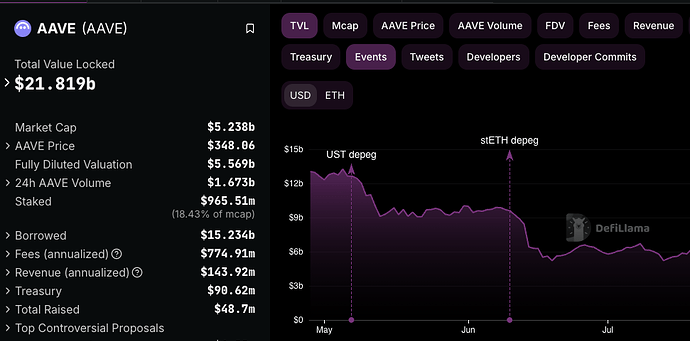
In mid 2022, Aave experienced a 50%+ drawdown in TVL following the UST and stETH depegs, outpacing the 30% drop in ETH over the period. This disparity is indicative of substantial amounts of withdrawals and loan closures.
While setting CFs too low could also lead to users withdrawing to seek better capital efficiency elsewhere, the rate of TVL loss tends to be much more gradual, with inelastic demand staying put.
Main takeaway
Raising CFs constrains the maximum LP, which reduces both the insolvency buffer and the incentive liquidators demand to cover their costs. For assets where LPs are already set to moderate or low levels, this directly leads to an increase in insolvency risk. In addition to the initial monetary loss, the risk can be further exacerbated by a bank run and brand damage.
LRT oracle selection
There’s been some discussion around oracles for LRTs, ranging from using Chainlink to adopting the correlated asset price oracle (CAPO) and killswitch from Aave. It might be helpful to review some of the tradeoffs of these choices.
Review
Intrinsic value vs market price
Because LRTs can be redeemed for the underlying, they have an intrinsic value that is tied to the price of the base asset. Changes in intrinsic value can occur from
- slashing
- loss of assets by operators e.g. hacks
- redemption freezes or changes in capacity or waittime of withdrawal queue
LRTs can also be traded in the open market on exchanges where they have a market price. These prices have natural volatility and can fall substantially in the event of panic selling or market manipulation.
Arbitrageurs
Arbitrageurs are incentivized to keep the market price in line with intrinsic value, but, similarly to liquidators, if their costs are not sufficiently covered by the profits, they are content to do nothing and let these values deviate.
Whereas most liquidations are transactions that atomically guarantee profit within the block, arbitrageurs often have significantly more uncertainty in their trades that stem from adverse selection, longer holding periods (e.g. tying up capital for a week in an LRT withdrawal queue), basis risk, opportunity cost and other factors.
As such, traders have risk limits and checks that often require human judgment to override, ensuring systems are not erroneously detecting market opportunities—a critical safeguard to avoiding blowups like Knight Capital. Response times tend to be longest during events that are both infrequent and high in dollar impact (e.g. LRT depeg) due to the unfamiliarity and stress on risk management systems.
Assumptions
Recursive borrowers using LRTs as collateral against the underlying asset find liquidations acceptable when driven by changes in intrinsic value but not when caused by drops in market price if the intrinsic value remains unchanged.
While Compound is likely more risk-averse than leveraged borrowers, holding loans that are underwater when marked to market price but solvent when marked to intrinsic value poses relatively low risk. We assume this is acceptable to the protocol for short durations e.g. on the order of a few blocks.
In essence, if both Compound and borrowers want LRT looping loans to persist when intrinsic value is stable, arbitrageur inattentiveness or failure within the oracle update window should not lead to the forced closure of these loans via liquidation.
Market rate
The most common type of oracle is a market rate oracle that aggregates node responses based on market data, typically prices across exchanges. This works well when prices are kept in line by arbitrageurs but can pose challenges for assets with lower liquidity.
As seen in the mainnet Chainlink ezETH / ETH oracle,
the sudden rate spikes and reversions were likely due to liquidity being primarily concentrated in this Balancer V2 stable pool, which had limited ezETH bid liquidity. When coupled with the 10% drawdown in ETH on Jan 13 or the 20% drop within an hour on Feb 2, this led to delays in arbitrageurs correcting the deviation.
In particular, ezETH is a ~1B market cap asset that usually only trades 5-10M a day and dislocating the price 10% might only cost ~500k. Using a market rate oracle for ezETH for a WETH lending comet would put users at significant risk of forced liquidations.
Staking rate
An increasingly popular choice for LRTs is to use a staking rate oracle, which tracks the intrinsic exchange rate between the LRT and the underlying asset. By removing the noise from market illiquidity, we could expect the plot of such a rate to look like the following:
a monotonically increasing trend with drawdowns occurring only due to slashing events. This is ideal for meeting the needs of both recursive borrowers and Compound, as any liquidations that occur would be as expected.
Staking rate oracles typically pull data directly from smart contracts specific to a given LRT. For example, the Compound III ezETH / ETH oracle queries the Renzo RestakeManager. Unlike market oracles, which are standardized by organizations like Chainlink or Pyth—and trusted due to their network design and brand reputation—staking rate oracles are custom written and must be audited individually.
In the case of ezETH, the oracle used by Compound III computes the ezETH/ETH rate using the getRate function of the BalancerRateProvider. This function derives the rate by dividing the output from the calculateTVLs function of the RestakeManager by the total supply of ezETH. If there is any lapse in accounting on deposits, withdrawals, claims, mints or redeems when tracking the outstanding LRT supply vs the TVL of the LRT across base asset and rewards, this could lead to an incorrectly reported rate, potentially resulting in unintended liquidations.
Risks
Manipulation
Regardless of whether a market rate oracle or a staking rate oracle is used, the primary risk comes from a malicious actor manipulating the oracle’s output by exploiting vulnerabilities in its computation logic.
Since market rate oracles provide an aggregated response based on exchange activity, a protocol using such an oracle is at risk of attack when the cost of market manipulation is lower than the potential profits from an economic exploit. When liquidity is scarce, this can lead to significant dislocations between market price and intrinsic value.
For reference, below is a comparison of the ezETH/ETH Chainlink oracle and the staking rate during the ezETH depeg last April, illustrating how large the deviation can become.
While the depeg was driven by panic selling and cascading liquidations—triggered by disappointing airdrop news and exacerbated by the absence of a redemption mechanism for ETH at the time—rather than outright manipulation, the existing market illiquidity for ezETH suggests that a similarly adverse price path could be deliberately orchestrated. Had Compound III been using the Chainlink oracle instead of the Renzo staking rate oracle, it likely would have experienced a substantial amount of undesired liquidations and insolvent debt.
Attacking staking rate oracles typically involves targeting smart contract logic rather than manipulating the market. Some common exchange rate manipulation attacks are described in this Euler blog post. Previous Renzo audits have identified vulnerabilities in earlier smart contract versions, including this ezETH exchange rate attack vector.
As the scale and likelihood of manipulation increase, larger insolvency buffers are needed to shield the protocol from losses. Features like the rate change safeguards in the EzETHPriceCapAdapter used by Aave help limit the magnitude of such attack vectors.
Variance
A secondary consideration is natural variability in oracle output. If the variance is high relative to the liquidation factor, highly levered users may face significantly higher liquidation risk than anticipated.
Below is a plot of the Compound III ezETH oracle, sampled for the past 90 days.
No slashing events occurred during this period, but some non-monotonicity can be attributed to the variability of LRT rewards that are not denominated in the base asset. Tracking these in the TVL require oracle lookups, where the RestakeManager makes a call to the RenzoOracle here, which queries Chainlink here. These market rate oracles exhibit higher volatility, and the assets themselves may have worse liquidity profiles.
As such, features like a killswitch—which automatically intervenes during large price movements or liquidity degradation—could help limit adverse effects on the protocol.
Main takeaway
The choice of oracle is a key determinant of both the leverage that can be safely offered to borrowers and the insolvency risk faced by a lending market.
For LRTs, oracles should rely on the staking rate rather than market rates like Chainlink, due to the unreliability of arbitrageurs being incentivized to keep markets in line in a timely fashion. This necessitates custom oracle feeds, which should undergo individual audits and incorporate necessary safeguards, such as CAPO.
Since LRTs accrue rewards that are valued based on their own market rates, additional features such as a killswitch are useful in mitigating the effects of market anomalies. Bounding the magnitude of tail risks allows the protocol to offer higher collateral factors.
Compound III design differences
In a community call, DoDAO pointed out that, all else being equal, Compound III CFs should be higher than Aave’s since Aave introduces additional risk from rehypothecation, which Compound III does not. Rehypothecation also provides Aave borrowers with yield on their collateral assets, a benefit they wouldn’t receive on Compound III.
While this statement is true in isolation, the main limiting factor for Compound III’s CFs is actually its liquidation design, which puts it at a disadvantage when competing with Aave V3 on collateral factors.
Review
Liquidations vs absorptions
For loans with a single collateral and borrow asset on Aave V3, the maximum borrowable amount is determined by the loan to value ratio (LTV), while liquidations are triggered when the debt-to-collateral ratio exceeds the liquidation threshold (LT).
During a liquidation, a portion of the borrower’s debt is repaid, and they forfeit the corresponding amount of collateral, scaled by the liquidation bonus (LB). Of this bonus, a liquidation protocol fee (LPF) is collected by the protocol, while the remainder is paid to the liquidator. Additionally, the amount of debt that a liquidator is allowed to repay in a single transaction is constrained by the close factor (c).
We can derive the following relationship
![]()
where the left hand side of the inequality is set to prevent opening loans that are immediately liquidatable and the right hand side is set to ensure liquidations improve the collateralization of the loan.
Comparing this to our earlier review of absorptions on Compound III we note some parallels
- LTV on Aave V3 is analogous to CF on Compound III
- LT corresponds to LF
- LB serves a similar purpose to LP
- LPF maps to 1 - SFPF
along with several key differences
- Compound III takes over the full position when absorb is called and pays out the difference between the debt and collateral sans liquidation penalty as base asset to the borrower out of the protocol reserves. This leads to warehousing a lot more immediate price risk compared to Aave V3 where the close factor ensures that liquidations occur more gradually
- The insolvency buffer on Compound III is independent of LF and entirely determined by LP and SFPF. On Aave V3 the insolvency buffer is dependent on LT, LB, LPF and c. As such, Aave V3 gets shielded from insolvency from the close factor and the gap between LT and maximum LT whereas Compound III does not
- Users lose more in liquidations on Compound III than on Aave V3 for the same LP / LB since the value of the liquidation payout in collateral asset terms is calculated as a multiplier on the debt i.e.
 on Aave V3 whereas on Compound III it’s a multiplier on the collateral i.e.
on Aave V3 whereas on Compound III it’s a multiplier on the collateral i.e. 
- The maximum LT on Aave is always higher than the maximum LP on Compound III for the same LB / LP. This can be seen since

Insolvency buffer
For Aave V3 we define the insolvency buffer (IB) as the maximum % the collateral price can drop relative to the debt between the loan being liquidatable and insolvent.
A derivation of the IB is attached for the interested reader
We’re interested in how raising LF/LT impacts the insolvency buffer for the two protocols. To help reduce dimensionality, let’s define the aggressiveness (a) of each protocol as
![]()
and
![]()
This ratio normalizes the LT and LF relative to their respective maximum values, providing a standardized measure of how aggressively the protocol is setting its risk parameters.
Currently, the highest aggressiveness on Aave V3 is just under 96.5% for wstETH, with a 95.5% LT and a 1% LB in the ETH correlated emode on their mainnet Prime market. For Compound III, the highest aggressiveness is slightly below 97% for weETH, with a 93% LF and a 4% LP in the mainnet WETH comet. Using these empirical values to set LB/LP based on LT/LF along with SFPF at 0.7 as per the mainnet WETH comet, LPF at 0.1 as set for ezETH and a close factor of 0.5 as set in the Aave V3 contracts produces the following plot.
As shown, with current parameters the insolvency buffer declines with higher liquidation factors as expected. More notably, the IB is substantially higher on Aave V3 than Compound III pretty much irrespective of LF [2].
This begs the question as to whether Compound III can make parameter changes to reduce or even flip this difference. Since both protocols are already near max aggression, the only parameter Compound III can really tweak is the store front price factor.
The difference in insolvency buffer between the Aave and Compound is minimized when SFPF = 0
[3] and also when c = 1. This is because IB for Aave V3 decreases as the close factor increases. Ultimately, when the close factor reaches 1, it becomes equivalent to not having a close factor at all [4].
Using these extreme parameters gives the following plot
Unfortunately, even in this extremely favorable setting, the insolvency buffer remains greater for Aave V3 across the board. However, it is worth noting that the gap is much smaller, highlighting the value of having a close factor to facilitate partial liquidations.
In practice, this scenario would almost never occur since it would essentially require liquidators to work for free while also disabling a key safety feature in Aave V3.
User costs
The protocol can also be examined from the lens of the cost to the user getting liquidated. By inverting the insolvency buffer equations above to solve for the liquidation penalty and converting costs to collateral terms, we obtain the following plot using the existing parameters.
For a fixed insolvency buffer, Compound III does eventually charge the user less than Aave V3, but only when the collateral cost exceeds ~65%. At all cost levels that a user would realistically find acceptable, Aave V3 charges less for the same insolvency buffer as Compound III.
Applying the same favorable extrema as before gives
The cost gap shrinks, but Compound III only overtakes Aave V3 when the collateral cost exceeds 35%, which is still too high in practice to be actionable. Even in this case, Aave V3 still outperforms Compound III in terms of user costs.
Leverage matching
As a concrete example of the results shown above, let’s examine what happens when we try to provide the same amount of leverage for ezETH on Compound III as is currently allowed on Aave V3.
Currently ezETH has an LTV of 0.93, LT of 0.95 and LB of 0.01 in LRT wstETH emode on Aave V3’s mainnet Prime market. This corresponds to an IB of ~5%.
Now, suppose Compound III raised CF and LF to 0.93 and 0.95, matching Aave V3. The maximum possible LP in this case is 0.05, which results in an IB of ~1.6% with the existing SFPF—less than 1/3 of Aave’s IB while incurring over 5× the user cost. To achieve IB parity with Aave by modifying the SFPF, it would need to be reduced from 0.7 to ~0.01. Additionally, SFPF is set per comet, rather than per asset so such a change would drastically affect all other collateral assets in the comet.
If Compound III were to match Aave V3 on user cost with an LP of 0.01, it would yield an insolvency buffer of ~30 bps, which is more than 16× smaller than Aave’s IB.
Alternatively, if Compound III attempted to match Aave V3’s IB by raising the LP, it would require an LP of nearly 0.15. Not only would this be >15× costlier to users than Aave, but it would also constrain the maximum CF to 0.85, reducing available leverage.
Main takeaway
Because of Compound III’s liquidation mechanism, it is essentially impossible in practice to match the leverage offered by Aave without either costlier liquidations for borrowers or a smaller insolvency buffer for the protocol.
Next steps
Despite the sobering takeaways there are still plenty of paths forward.
Existing solutions
Compound III
On the existing protocol, one approach would be to have isolated comets with one collateral asset per comet in an extreme case or a group of LRT/LSTs as collateral assets all for the same comet asset. The existing WETH comet would have a risk profile that is more conducive to raising CFs if less correlated collateral assets, like WBTC, were placed in separate comets. Currently, these assets share a store front price factor with ETH LRTs, but their optimal values in isolation are likely quite different.
In the case of ezETH, the largest day over day drawdown over the last 90 days for the Compound III oracle was <20 bps so raising CFs in an isolated setting seems reasonable. Separating collateral across comets reduces the risk profile [5] for base asset lenders but fragments liquidity. If lenders are interested in a specific particular opportunity e.g. lending to recursive ezETH borrowers, then this approach could enable a more capital-efficient bilateral market without introducing additional risk to the rest of the protocol.
Compound V2
After disabling the UAV, Compound V2 may be a better choice for isolated LRT markets from a design perspective. V2 can use the same staking rate oracles as V3 but has a liquidation mechanism that closely resembles Aave’s and has a close factor. Compared to V3, this would reduce liquidation costs for borrowers while maintaining a stronger insolvency buffer for the protocol.
Collaborations
Proposals like this suggested collaboration with Morpho on Polygon could allow Compound to better compete without requiring new smart contract development. Morpho has isolated markets and has curators such as Gauntlet dynamically optimize risk adjusted yield for lenders by continuously reallocating liquidity across high demand markets.
New features
The list of new features to add to the protocol is extensive so will only give a few suggestions. Would be glad to join the conversation about what to prioritize in terms of expected impact vs development cost.
Liquidations
- The store front price factor is set for the entire comet but having it be set on a per asset basis allows for better risk parameterizations that enable more capital efficiency
- A close factor would increase the insolvency buffer and reduce borrower liquidation costs
- Soft liquidations where the close factor is dynamic based on collateralization should have a similar effect and have worked well on Euler in the past, especially in driving down user costs without compromising much on insolvency risk
Oracles
- Having conservative valuations for collateral and aggressive valuations for debt at loan origination protects against adversarial attacks as noted here following the Compound V2 UAV incident
- Generally the gap between these two valuations should be small but the gap becoming large is indicative of attack possibility
- The confidence intervals from Pyth oracles can be utilized to implement this like on Synonym
- CAPO and killswitch are both good features for mitigating tail risk which allows the protocol to safely offer more leverage
Hope this was a helpful overview. Happy to discuss further on the next community call.
There is the case where LPs are set too high to the point where lowering them mitigates insolvencies caused by cascading liquidations. ↩︎
As an aside, the x-axis cuts off at 70% LF since with these aggression values LFs below 70% correspond to unrealistically high LPs (30%+). ↩︎
- ↩︎
This also does occur when loan collateralization drops below 95% of LT. ↩︎
As an example, if a WETH comet enables weETH, ezETH and ezETH as collateral a WETH lender is exposed to insolvency risk across all the assets, especially from toxic loans being opened in slash events. The adverse selection here could be particularly bad if there is temporal correlation in slashes that provide leading indicators before the oracle update. ↩︎